Quantitative Aptitude Quiz For SBI PO/Clerk Prelims
Q1. In eleven hours C walks 12.5 km less than what D covers in twelve hours; and in five hours D walks 3.25 km less than what C covers in seven hours. How many km does each walk per hour?
Q2. Two trains pass each other on parallel lines. Each train is 100 metres long. When they are going in the same direction, the faster one takes 60 seconds to pass the other completely. If they are going in opposite directions, they pass each other completely in 10 seconds. Find the speed of the slower train in km/hr.
Q3. At 9 am Sunny steals a mobile of Satish and ran away with speed 45 kmph. At 11 AM Satish started chasing and catches Sunny at 5 pm. Find the speed of Satish.
Q4. Prince reaches office from home 12 minute early if he goes with speed of 15 kmph. He reaches office 20 minute late if he travels with speed 9 kmph. Find the distance between his office to home.
Q5. A train running with 54 km/hr can cross an electric pole in 40 sec. If the train increases its speed by 20% then in how much time it can cross a 750m long platform.
Q6. Anurag travels ⅓ of his journey with speed 50 kmph. 40% of the remaining distance with speed 40 kmph and rest with speed 90 kmph. Find the average speed of his journey.
Q7. Two trains running in opposite directions to each other, cross a man standing on the platform in 30 sec and 12 sec respectively and they cross each other in 20 seconds. Find the ratio of their speed.
Q8. A 320 metres long train takes 80 seconds more time to cross a platform than it takes to cross a pole at the same speed. If the length of platform is twice the length of train, then find the speed of the train.
Q9. Train A which is 320m long crosses a pole in 16 seconds. If it halts 5 times each time for exactly 18 minutes, how many hours will it take to cover a distance of 576 km?
Q10. A train overtakes two persons walking along a railway track. The first one walks at 4.5 kmph. The other one walks at 5.4 kmph. The train needs 8.4 and 8.5 seconds respectively to overtake them. What is the speed of the train if both the persons are walking in the same direction as the train?
Q11. A train passes two persons who are walking in the direction opposite to the direction of train at the rate of 10 m/s and 20 m/s respectively in 12 seconds and 10 seconds, respectively. Find the length of the train.
Q12. A thief steals a car at 2.30 pm and drives it at 60 kmph. The theft is observed at 3 pm and the owner sets off in another car from same place at 75 kmph. When will he catch the thief?
Relative speed = (75–60) = 15 kmph
Distance to be covered = 30 km
Hence, time taken by the owner in catching the thief
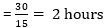
Therefore, owner will catch the thief at 2 hours after 3 pm i.e. at 5 pm
Directions (13-15): What should come in place of question mark (?) in the following number series?
Q13. 12, 12, 18, 36, 90, 270, 945, ?
Q14. 444, 467, 513, 582, 674 , 789, ?
Q15. 8, 10, 23, 73, 297, ?





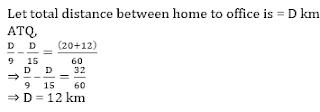


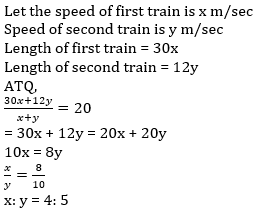

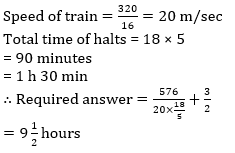

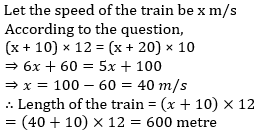
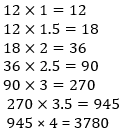
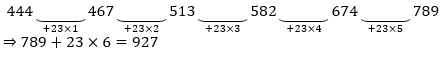
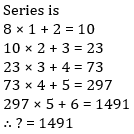


 The Hindu Review October 2022: Download ...
The Hindu Review October 2022: Download ...
 IBPS Calendar 2024 Out, Download IBPS Ex...
IBPS Calendar 2024 Out, Download IBPS Ex...
 IBPS SO Final Result 2024 Out, Download ...
IBPS SO Final Result 2024 Out, Download ...



