Quantitative Aptitude Quiz For NIACL AO
Directions (1-5): In the given questions, two quantities are given, one as ‘Quantity 1’ and another as ‘Quantity 2’. You have to determine relationship between two quantities and choose the appropriate option:
Q1. A is twice as efficient as B. Both can complete a work together in 7½ days.
Quantity 1: Time taken by B to complete the work alone.
Quantity 2: If C is 50% more efficient than A, then time taken by C to complete the work alone.
Q3. Two dices are rolled simultaneously. Quantity 1: Probability that the sum of the numbers that appeared is a multiple of 5. Quantity 2: 1/6
Q4. Sum of height and diameter of the cylinder is 28 meter. Quantity 1: Curved surface area of the cylinder whose respective ratio of height to diameter is 3 : 4 Quantity 2 : Curved surface area of the cylinder if height of cylinder is 10 m.
Q5. Product of digits of a two digits number ‘N’ is 21 Quantity 1 : N Quantity 2 : 130–N
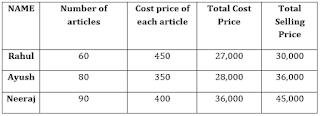
Directions (6-10): Data given below shows total articles sold by three retailors. Study the data carefully and answer the following questions.
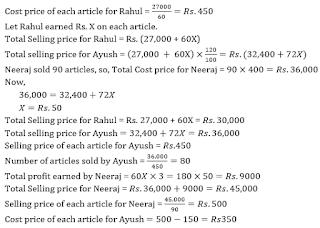
Rahul → Total cost price of 60 articles is Rs. 27,000
Ayush → Total selling price for Ayush is 20% more than total selling price for Rahul. And selling price of each article for Ayush is same as Cost price of each article for Rahul. Cost price of each article for Ayush is Rs.150 less than Selling price of each article for Neeraj.
Neeraj → Total profit earned by Neeraj is thrice than that of total profit earned by Rahul and sold 30 articles more than Rahul. Total cost price for Neeraj is same as total Selling price for Ayush. Cost price of each article is Rs.400 for Neeraj Total Selling Price = Total Cost Price + Total Profit Total Cost Price = Number of articles sold × Cost Price of each article
Q6. Find total profit earned by Ayush?
Q7. Average number of articles sold by Rahul, Ayush, Neeraj and Satish is 85. Find total number of articles sold by Satish?
Q8. Cost price of each article for Ayush is what percent more/less that Selling price of each article for Rahul?
Q9. Out of total articles sold by Neeraj and Ayush, 30% and 50% were defective respectively. Find total number of non-defective articles sold by Neeraj and Ayush together?
Q10. Find the ratio between total selling price for Rahul to total Selling price for Neeraj?
Q11. Mixture containing milk and water in ratio of 2 : 3 has volume of 30 liters. If 10 L of water is added to it then find the ratio of milk to water in the mixture?
Q12. Average weight of 10 boys in a class is 56 kg and that of 5 girls is 54 kg. Two boys of 54 kg and 78 kg respectively and a girl of 55 kg left the class. Find the average of remaining students in that class.
Q13. The circumference of two circles is 132 m and 176 m respectively. What is difference between the area of larger circle and smaller circle ? (in m²)
Q14. Average of four numbers is 26. Sum of the smallest and the largest number is 55. If difference between other two numbers is one then find the square of second smallest number.
Q15. The average age of Ram and his son, five years ago was 27.5. Ram’s present age is five years more than thrice of his son’s present age. Find ratio of their present ages?


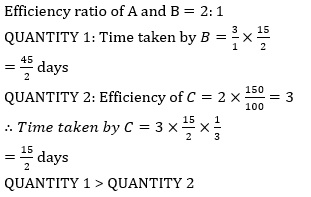
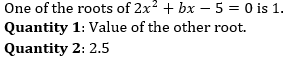
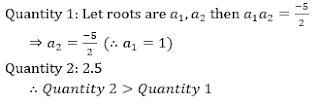



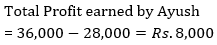
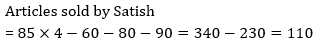
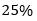
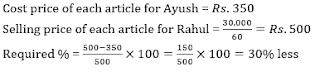
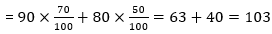
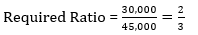
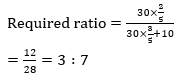
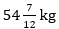
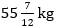
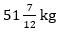
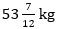
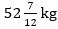
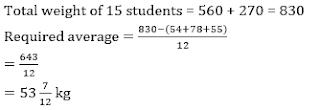


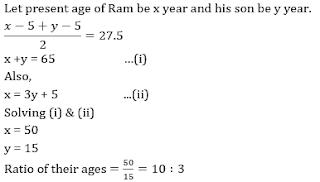


 The Hindu Review October 2022: Download ...
The Hindu Review October 2022: Download ...
 World Intellectual Property Day 2024, Th...
World Intellectual Property Day 2024, Th...
 SBI SO Salary 2024, Salary Structure, Pe...
SBI SO Salary 2024, Salary Structure, Pe...



