List of Important Maths Formulas For Bank Exams 2023

Math Formulas For Bank Exams

The mathematical section of competitive banking entrances is comprised of a lot of facts and figures. Most importantly, the candidate has to deal with many crucial formulas to crack the exams with good scores. The quantitative approach of the students gets flourished with the Maths Formulas For Bank Exams. Most of the time, aspirants need clarification about using the right mathematical formulas.

So, here we are delivering the best and chosen knowledge of formulas as per the syllabus of banking exams. Some crucial mathematical elements in banking exams include sum, fractions, averages, decimal numbers, and percentages. Here, we have enlisted the most authentic Maths Formulas for Bank Exams you can refer to.

Math Formulas

If you are willing to crack banking exams like SBI Clerk, SBI PO, IBPS RRB Officer Scale, IBPS Clerk, or RBI, you need to strengthen your proficiency in mathematical skills. So, here we list some efficient Maths Formulas for Bank Exams for you to look at. These formulas will help you solve the maths section easily in a specific time frame. Energise your basic maths skills by learning these formulas for any banking exam.

List of Important Math Formulas for Bank Exams

If you want to acquire the best score in the mathematics section of banking exams, listed below are some helpful formulas. We have categorised the sections to give you a precise understanding of the formulas.

Number System

The number system is a comprehensive part to score more in any banking exams. It is used to value the information in a quantitative manner. some of the integral types of number systems are,

• Binary Number System
• Decimal Number System
• Octal Number System
• Hexadecimal Number System.

The values of a specific digit can be recognized by

• Its position in the number
• The actual digit
• The base of the number system

Natural Numbers:

Numbers that are utilized for counting objects are termed Natural numbers. The natural numbers are signified by N.

N = {1, 2, 3, 4…………}

Whole Numbers:

Whole numbers are the set of numbers in which zero and natural numbers are involved. The whole numbers are presented by W.

W = {0, 1, 2, 3, 4…….}

Integers:

Integers involves all natural numbers in addition to zero & negative numbers. Integers are denoted by I or Z.

I = {-3, -2, -1, 0, 1, 2, 3…..}

Rational Numbers:

Rational numbers are expressed in the form of p/q where ‘p’ & ‘q’ are integers and q≠0. They are denoted by Q.

Q = 5/6, 7/8 etc.

Irrational Numbers:

The numbers which cannot be expressed in the form of p/q where ‘p’ & ‘q’ are integers and q≠0. They are denoted by Q.

Example – π = 3.141592653589793238….
Even Numbers:
The numbers which are divisible by 2 are known as even numbers.
Example – 2, 4, 6, 8, 10….
Odd Numbers:
The numbers which are not divisible by 2 are known as odd numbers.

Ratio and Proportion

When we get involved in comparing two quantities, either encounter the difference (a-b) or we go for division. When we go for dividing two numbers to acquire the magnitude of one in comparison to another we name it as a ratio. The ration of two digits will be represented as ‘a:b’. The formulas to remember for Ratio and Proportion are listed below.

Ratio Formula: a:b->a/b

Proportion Formula: a:b :: c:d -> a/b=c/d

Properties of Ratio

1. Ratio remains the same when you multiply or divide both the quantities with the same non- zero number. 

• a:b=pa:pb=qa:qb
• a:b=a/p:b/p=a/q:a/q

Where p=q≠0

1. We can compare two ratios as real number in their fraction form

a:b=p:q ⇔ aq=bp

• a:b>p:q ⇔ aq>bp
• a:b

1. If two ratios are equal

• a:b=p:q ⇔ b/a=q/p (invertendo)
• a:b=p:q ⇔ a/p=b/q (Altertendo)
• a:b=p:q ⇔ (a+p)/p=(b+q)/q (componendo)
• a:b=p:q ⇔ (a-p)/p=(b-q)/q (dividendo)

• Properties Of Proportion

1. Product of extremes = product of means i.e., ad = bc
2. a, b, c, d,…. are in continued proportion means, a:b = b:c = c:d
3. a:b = b:c then b is called mean proportional and b2 = ac
4. The third proportional of two numbers, a and b, is c, such that, a:b = b:c
5. d is fourth proportional to numbers a, b, c if a:b = c:d.
6. The two terms ‘b’ and ‘c’ are known as ‘means or mean terms’, on the other hand the terms ‘a’ and ‘d’ are known as ‘extremes or extreme terms.’

Percentage

Percentage is considered as per hundred. Percentages are known to be the portion of 100 and is signified with a % symbol. Percentage is simply utilized to find and compare ratios. It is a scoring topic if you will learn it effectively. If you are willing to crack any banking exams, learn these percentage formulas to elevate your overall score.

Formulas:

Percentage formula

The comprehensive formula to get the number of percentages has to divide the number by the value of total sum and them multiply it with 100.

Percentage of a number

To evaluate the percentage of a number, the formula used is A% of Number = B. Here, B is the needed percentage. When the % sign is extracted, the following formula will be, A/100 * Number = B.

Percentage Tricks

One of the effective trick to calculate percentage is a% of b = b% of a.

 

Mixtures and Alligations

An aggregate of 2 or more types of quantities denotes a mixture. on the other hand Alligation is a method to solve arithmetic equations linked to mixtures of ingredients. The formulas of Mixture and alligations helps us to find the weighted average. This topic can make you get good score in your banking exam as you can solve these equations in a less time frame.

Formulas:

The compelling formula which is utilized to calcuate the ratio in which the ingredients are mixed is listed below:

This formula is also known as rule of alligation which can be also represented as,

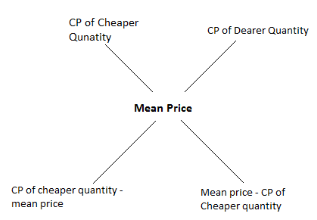
Profit and Loss

We all know that the significance of Profit and Loss section is extremely integral in Banking exams. A student must prioritize the importance of profit and loss to get good grades in banking exams. It signifies the concept where an individual gets or lose money when purchasing or selling it. Some of the effective formulas of profit and loss has been listed below.

Formulas:

• Profit = Selling Price – Cost Price.

Profit percentage (P%) = (Profit /Cost Price) x 100.

• Loss = Cost Price – Selling PriceLoss percentage (L%) = (Loss / Cost price) x 100.
• Discount = Marked Price – Selling PriceDiscount Percentage = (Discount/Marked price) x 100.

Simple Interest and Compound Interest

Simple Interest is reliable on the principal amount considered for a deposit or a loan. On the other hand, compound interest is regarded as a principal amount and the interest functions over every period. Some of the crucial formulas of this topic has been mentioned below for your reference.

Formulas: For Simple Interest

SI = P x R x T/100 

•  Principal = Simple Interest ×100/ R × T
•  Rate of Interest = Simple Interest ×100 / P × T
• Time = Simple Interest ×100 / P × R
• If the rate of Simple interest differs from year to year, then

Simple Interest = Principal × (R1+R2+ R3…..)/100

( SI=Simple Interest P=Principal Amount (This the amount invested)T=Number of years R=Rate of interest (per year) in percentage).

Formulas: For Compound Interest

The difference between the amount and the money borrowed is called the compound interest for a given period of time

•  Let principal =P; time =n years; and rate = r% per annum and let A be the total amount at the end of n years, then A = P*[1+ (r/100)]ⁿ;

CI = {P*[1+ (r/100)]ⁿ -1}

• When compound interest reckoned half-yearly, then r% become r/2% and time n becomes 2n; A= P*[1+ (r/2*100)]²ⁿ

For the quarterly, A= P*[1+ (r/4*100)]⁴ⁿ

The difference between compound interest and simple interest over two years is given by,

Pr²/100²or P(r/100)2

• The difference between compound interest and simple interest over three years is given by,

P(r/100)²*{(r/100)+3}

Time and Distance

When it comes to banking exams, time and distance is considered to be the most crucial factor. Moreover, it is one of the easiest topic that everyone can deal with. The types of questions from this section may vary as per the sections. So, we have enlisted all the formulas below to make it easy for you to score good.

Formulas:

Speed = Distance/TimeTime =Distance/Speed
Distance = (Speed × Time)
Average Speed= Total Distance / Total Time
1 km/hr = 5/18 m/sec
1 m/sec = 18/5 km/hr
If the ratio of the speeds of A and B is a: b, then the ratio of the times taken by them to cover the same distance is 1/a: 1/b =b: a
If a man covers a specific distance at x km/hr and an equal distance at y km/hr. Then, the average speed for the total journey will be (2xy /x+y) km/hr.

Permutation and Combination

Permutation is known to arrange all the crucial elements of a set into a sequence. on the other hand combination is known to be a system of picking elements through a collection. Here we have enlisted some important formulas related to permutation and combination you need to know to crack any type of banking exams.

Formulas: For Permutation

In permutation, we opt for the things and then safely arrange them to verify  different ways of arrangements. So, permutation can be valued as a two-step process.

The formula used for permutation is ⁿP_r = n!/(n-r)!

Formulas: For Combination

In combination, we prefer the things randomly & verify the different ways of selection. So this is known to be a one step process. Combination is also regarded as collection. The formula utilized for combination is ⁿC_r.

ⁿC­_r = n! / [r! x (n-r)!]

ⁿC­_r = [n x (n-1) x (n-2) x (n-3) x……x(n-r+1) x (n-r) X…….x 1] / [1x 2 x 3….. x r] X [(n-r) x……..3 x 2 x 1]

ⁿC­_r = [n x (n-1) x (n-2) x (n-3)….. x (n-r+1)] / [1x 2 x 3….. x r].

Data Interpretation

Data Interpretation is a topic through which we can understand the data to get factual interferences with proper analysis of the data. So, data management is a crucial addition into any banking exams. You need to be careful about time management when working with data interpretation. Here we have enlisted some effective formulas to help you in your next banking exam.

Formulas:

• Percentage: Percentage = (Part / Whole) x 100
• Average: Average = (Sum of all values) / (Number of values)
• Profit/Loss: Profit = Selling Price – Cost Price Loss = Cost Price – Selling Price Profit/Loss Percentage = (Profit/Loss / Cost Price) x 100
• Compound Interest = Principal x [(1 + Rate/100) ^ Time] – Principal
• Simple Interest: Simple Interest = (Principal x Rate x Time) / 100
• Ratio and Proportion: If two quantities are in a ratio of a:b, their proportion can be expressed as a:b or a/b.
• Percentile: Percentile = (Number of values below a certain value / Total number of values) x 100.

Time and work & Pipe and cistern

Words problems based on Time and Work or Pipe and Cistern is common over the quantitative section of banking exams. Pipes and cistern is a well-composed format for solving time and work related questions. Some of the effective type of questions from this topic are time taken to fill a tank and amount of work done. So, to make you eminent in his topic we have listed out some important formulas that you will definitely see in your upcoming banking exams.

Formulas:

• If x hours are valued to fill up a tank, then part filled in 1 hr =1/x
• If y hours are needed to empty the tank, then part emptied in 1 hour = 1/y
• If a pipe can fill a tank in x hours and can empty the same tank in y hours. When both the pipes are opened at the same time, then the net part of the tank filled in 1 hr = {(xy) / (x-y)}, provided x>y
• If a pipe can fill a tank in x hours and can empty the same tank in y hours. When both the pipes are opened at the same time, then the net part of the tank filled in 1 hr = {(xy) / (y-x)}, provided y>x
• Net work done = (Sum of work done by Inlets) – (Sum of work done by Outlets)
• One inlet can fill the tank in x hr and the other inlet can fill the same tank in y hrs, if both the inlets are opened at the same time, the time taken to fill the whole tank = {(xy) / (y+x)}
• If two pipes take x and y hours respectively to fill a tank of water and a third pipe is opened which takes z hours to empty the tank, then the time taken to fill the tank = {1 / (1/x)+(1/y)+(1/z)} and the net part of the tank filled in 1 hr = (1/x)+(1/y)-(1/z).

Time and Distance Boat and Stream

When it comes to Time and distance &Boat and Streams questions there is a vast range of sub concepts involved in it. It is important for any candidates to understand the prominent formulas of Boat and Stream questions to score well in any banking exams. Here we have listed down some crucial formulas for you to remember before approaching any banking exam.

Formulas: For Upstream and Downstream

Upstream = (u−v) km/hr.

Downstream = (u+v)Km/hr.

Speed of Boat in Still Water = ½ (Downstream Speed + Upstream Speed)

Average Speed of Boat = {(Upstream Speed × Downstream Speed) / Boat’s Speed in Steal Water}

Speed of Stream = ½ (Downstream Speed – Upstream Speed)

Average Speed of Boat = {(Upstream Speed × Downstream Speed) / Boat’s Speed in Steal Water}.

Mensuration

Mensuration is considered to be a crucial branch of Mathematics that involves studying the measurements and geometric figures and parameters such as volume, length, surface area, lateral surface area and more. Any banking exam consist of many questions from the mensuration section. Here we have listed out some effective formulas.

Formulas: Mensuration Formulas for 2D Shapes

Shape	Area (Square units)	Perimeter (units)
Rectangle	l × b	2 ( l + b)
Square	a2	4a
Circle	πr2	2 π r
Scalene Triangle	√[s(s−a)(s−b)(s−c)],Where, s = (a+b+c)/2	a+b+c
Isosceles Triangle	½ × b × h	2a + b
Right Angle Triangle	½ × b × h	b + hypotenuse + h
Equilateral triangle	(√3/4) × a2	3a
Rhombus	½ × d1 × d2	4 × side
Parallelogram	b × h	2(l+b)
Trapezium	½ h(a+c)	a+b+c+d

Mensuration Formulas for 3D Shapes

Shape	Volume (Cubic units)	Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units)	Total Surface Area (TSA) (Square units)
Cube	a3	LSA = 4 a2	6 a2
Sphere	(4/3) π r3	4 π r2	4 π r2
Cuboid	l × b × h	LSA = 2h(l + b)	2 (lb +bh +hl)
Hemisphere	(⅔) π r3	2 π r 2	3 π r 2
Cone	(⅓) π r2 h	π r l	πr (r + l)
Cylinder	π r 2 h	2π r h	2πrh + 2πr2

 

Probability

Probability is known to be the vast subject of Mathematics that is used to acquire numerical description of how likely an event is going to occur. However, the types of situational questions differ from one exam to other. We have listed out some integral formulas of probability through which you can solve every types of questions in a particular time frame.

Formulas:

You need to be thorough about the events for which you want to verify the probability for. Here we have enlisted some crucial formulas of Probability through which acquiring solutions will be easy.

• Event (A NOT B)

P(A NOT B) = A – B

• Event (A OR B)

P (A U B) = P (A) + P (B) – P (A ∩ B)

• Event (A AND B)

P (A ∩ B) = P (A) . P (B)

• Event (B NOT A)

P(B NOT A) = B – A

• Event (NOT A)

Probability of occurrence of an event is P(A). Probability of non-occurrence of the same event is P(A’).