Quantitative Aptitude Quiz For IBPS PO Mains 2022-19th January |

Directions (1-3): In the given questions, two quantities are given, one as Quantity I and another as Quantity II. You have to determine relationship between two quantities and choose the appropriate option.

Q1. Seven HR’s and Seven CEO’s are to be arranged in arow while seating in a seminar.
Quantity I – No. of way to arranged Seven HR’s and Seven CEO’s such that no two HR’s and no Two CEO’s adjacent to each other.
Quantity II – No. of way to arranged 7 HR’s and 7 CEO’s such that all CEO’s sit together.
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or no relation

Q2.Quantity I – when length and breadth of a rectangle increase by 2 cm. Area of rectangle increase by 84 cm². If breath decrease by 3 cm area decrease by 72 cm². Find perimeter of rectangle?
Quantity II – Radius of a cylinder is 14 cm² and height is 56 cm. Find how many Sphere can be formed from cylinder, if radius of sphere is half of the radius of cylinder.
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or no relation

Q3. There is five munch, four five stars and three KitKat chocolate in a bag A boy take out four chocolates randomly from the bag.
Quantity I – Probability ofselecting two munch and two five stars
Quantity II – Probability of two munch one five store and one KitKat
(a) Quantity I > Quantity II
(b) Quantity I < Quantity II
(c) Quantity I ≥ Quantity II
(d) Quantity I ≤ Quantity II
(e) Quantity I = Quantity II or no relation

Directions (4-8): Given below is the table which shows five different schemes and rate of simple interest (S.I.) and rate of compound interest (C.I.) offered on different schemes. All the interest rates are calculated annually.
Note : All the interest is calculated annually.

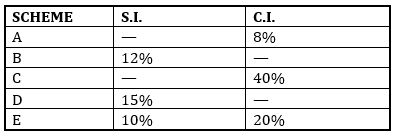
Q4. If a sum is invested in scheme B at C.I, then amount obtained after 2 year from this scheme is 1.44 times the sum invested. Rate of simple interest for scheme A is half of the rate of compound interest for scheme B. Find out the interest earned when 8000 was invested in each scheme mentioned above for 2 years.
(a) 5120
(b) 5000
(c) 4800
(d) Can’t be determined
(e) None of these

Q5. A man invested 10,000 in scheme D at S.I. for 6 month, the interest he obtained is divided into equal halves and invested in two different schemes i.e. scheme B and scheme C for 4 year each at S.I. If the ratio of interest obtained in both scheme is 3 : 2, then find out the rate of interest of C scheme.
(a) 10%
(b) 8%
(c) 11%
(d) 5%
(e) None of these

Q6. A sum is invested in scheme E at S.I. for 2 year and then whole amount obtained is invested at C.I. in same scheme for 2 more years. If same sum would have been invested in scheme D for 4 year with S.I. then, what would have been the ratio of amount obtained from scheme E to the amount obtained from scheme D.
(a) 27 : 25
(b) 21 : 23
(c) 40 : 49
(d) Can’t be determined
(e) None of these

Q7. A man invests equal sum in two different schemes, D and E at S.I. for 4 year each. The total interest he got is invested in the scheme A for 3 year at C.I. Due to some reason instead of getting interest from scheme A , the scheme is flopped and sum invested in scheme A is depreciated each year with same rate, and he got Rs. 778688 after 3 year. Find the amount he invested in both scheme initially.
(a) 30,00,000
(b) 40,00,000
(c) 20,00,000
(d) 10,00,000
(e) None of these

Q8. A sum is invested in scheme C for 5 years at S.I. and then the amount received from it is invested in same scheme for 2 years at C.I. Total amount received from the investment at CI is 194% more than the sum invested initially. Find out the rate of interest in scheme C for S.I.
(a) 10%
(b) 12.5%
(c) 15%
(d) 5%
(e) None of these

Directions (9-10): A box contains two types of ball i.e., red and Blue. Probability of choosing one red and one blue ball is 1/2 while probability of choosing two red balls is 3/20.

Q9. Find the probability of selecting two balls without replacement from the box such that at least one of them is red?
(a) 9/20
(b) 11/20
(c) 13/20
(d) 17/20
(e) 3/4

Q10. If 5 Red balls and 6 blue balls are added in the box, then find the probability of choosing two blue balls from the box at present?
(a) 1/2
(b) 1/3
(c) 1/4
(d) 1/5
(e) 1/6

Solutions