Table of Contents
Ratio and Proportion is a fundamental topic in the Quantitative Aptitude section of the BOB Office Assistant Exam 2025. Understanding this concept not only helps you solve direct questions but also forms the base for other important topics like mixtures, time & work, partnerships and percentages, and also helps in solving Data Interpretation. This article covers the key concepts, formulas, types of questions, and preparation tips for mastering Ratio & Proportion effectively.
Ratio & Proportion for BOB Office Assistant Exam 2025
Ratio and Proportion is a scoring topic if the basics are clear. For the BOB Office Assistant Recruitment 2025, focus on mastering fundamental concepts, practising regularly and analysing errors. With proper strategy and consistency, candidates can ace this topic and strengthen their overall aptitude section score.
What is a Ratio?
A ratio is a way of comparing two quantities by division. It tells how many times one quantity is contained in another. The ratio of two numbers a and b is written as:
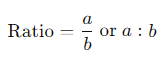
Example: If there are 2 apples and 3 oranges, the ratio of apples to oranges is 2:3.
What is Proportion?
A proportion is an equation that states two ratios are equal.
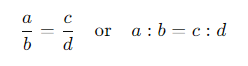
Example: If 2:3 = 4:6, then these two ratios are in proportion.
Ratios
A ratio compares two quantities of the same kind in their simplest form, showing how many times one value contains another.
| Key Properties of Ratios | ||
| Property | Explanation | Example |
| Same Units | Quantities must be in the same units before comparison | ₹5 to ₹10 = 1:2 (correct) 50cm to 2m = 50:200 = 1:4 (after conversion) |
| No Zero | The denominator can never be zero | 5:0 is invalid |
| Order Matters | a:b ≠ b: a unless a=b | 3:4 ≠ 4:3 |
| Invariant to Scaling | Multiplying/dividing both terms by the same number gives an equivalent ratio | 2:3 = 4:6 = 6:9 |
Types of Ratios
| Types of Ratios | ||
| Type | Formula | Application |
| Duplicate Ratio | (a:b)² = a²:b² | Used in area calculations |
| Triplicate Ratio | (a:b)³ = a³:b³ | Used in volume problems |
| Sub-duplicate Ratio | √a : √b | Geometric mean problems |
| Sub-triplicate Ratio | ³√a : ³√b | Volume scaling |
| Compound Ratio | (a:b) × (c:d) = ac:bd | Combined effect problems |
Proportion
When two ratios are equal, they form a proportion: a : b :: c : d or a/b = c/d
| Properties of Proportion | ||
| Property | Mathematical Form | Explanation |
| Alternendo | If a:b = c:d → a:c = b:d | Swapping means/extremes |
| Invertendo | If a:b = c:d → b:a = d:c | Inverting both ratios |
| Componendo | If a:b = c:d → (a+b):b = (c+d):d | Adding denominator |
| Dividendo | If a:b = c:d → (a-b):b = (c-d):d | Subtracting denominator |
| Componendo-Dividendo | If a:b = c:d → (a+b)/(a-b) = (c+d)/(c-d) | Powerful shortcut for problems |
Other Cases of Proportion
1. Continued Proportion: Three quantities a, b, c are in continued proportion if:
a:b = b:c → b² = a×c
Here, b is the mean proportional between a and c.
2. Fourth Proportional: For a:b = c:d, d is the fourth proportional:
d = (b × c)/a
3. Third Proportional: For a:b = b:c, c is the third proportional:
c = b²/a
Important Formulas & Shortcuts for Ratio & Proportion
Master these key formulas and shortcuts to solve the Ratio & Proportion problems quickly in Bank of Baroda Office Assistant Exam:
Ratio Formulas:
1. Combining Ratios: If A:B = a:b and B:C = c:d, then A:B:C = (a×c):(b×c):(b×d)
2. Dividing a Quantity: To divide Q in ratio a:b:c:
First part = a/(a+b+c) × Q
Second part = b/(a+b+c) × Q
3. Percentage to Ratio Conversion: 25% = 25:100 = 1:4
Proportion Shortcuts
1. Unitary Method: If 5 books cost ₹100, then 8 books cost (100/5)×8 = ₹160
2. Mean Proportional Trick: For numbers a and b, mean proportional = √(a×b)
3. Componendo-Dividendo Applications: Perfect for solving equations like:
(x+3)/(x-2) = 4/3 → Apply C&D to find x=17
Tricks to Solve Ratio & Proportion for BOB Office Assistant Exam 2025
Mastering Ratio & Proportion for the Bank of Baroda (BOB) Office Assistant Exam 2025 requires smart tricks to save time.
Trick 1: The Ratio Change Concept: When a quantity is added/removed from a ratio:
Problem: The ratio of boys to girls is 3:2. If 5 boys leave, the ratio becomes 1:1. Find original numbers.
Solution:
Original ratio: 3:2
After change: (3x-5)/2x = 1/1
Solve: 3x-5 = 2x → x=5
Original numbers: 15 boys, 10 girls
Trick 2: The Equalization Method: For problems with multiple ratios:
Problem: A:B = 2:3, B:C = 4:5. Find A:B:C.
Solution:
Make B’s value the same in both ratios (LCM of 3 & 4 = 12)
A:B = 8:12, B:C = 12:15
Final ratio: 8:12:15
Trick 3: The Replacement Formula: For mixture problems:
Formula: Quantity replaced = Total × (1 – (Original Ratio/New Ratio))
Common Mistakes to Avoid while Solving Ratio and Proportion
- Unit Mismatch: Always convert to the same units (km to m, hours to minutes)
- Order Confusion: Remember 3:4 ≠ 4:3 unless quantities are equal
- Over-Simplification: Don’t cancel terms prematurely in proportion problems
- Zero Denominator: Ratios like 5:0 are mathematically invalid
Preparation Tips for Ratio & Proportion
- Understand the Basics: Start with basic definitions, then move to solving simple examples.
- Learn Shortcuts: Use cross multiplication and ratio simplification tricks to save time.
- Practice Word Problems: Solve daily-life-based questions like income-expenditure, profit-sharing, etc.
- Solve Previous Year Papers: This helps you understand the exam-level difficulty and patterns.
- Mock Tests & Timed Practice: Practice under exam conditions to improve speed and accuracy.
Number Series Questions for SBI PO Exam
Simplification Questions for SBI PO Exam
Simplification Questions for SBI Clerk 2...
