Direction (1 -5): Given below line graph which shows number of days taken by six persons A, B, C, D, E and F to complete a work individually. Give answer of the questions according to graph and data given in questions —
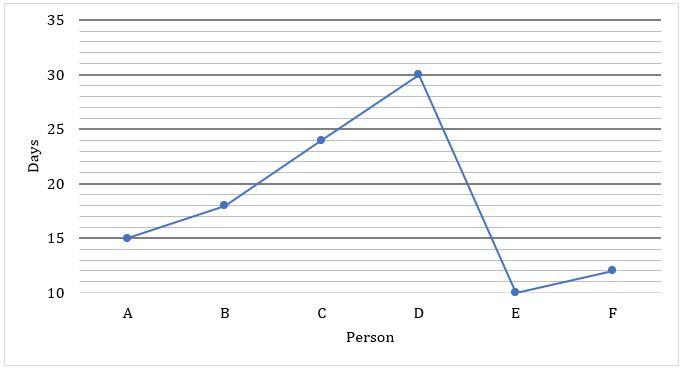
Q1. A worked for X days and then he left the work. After A left, B & D took responsibility of the work and completed the remaining work in (x+2 ½ ) days. Ratio of work done by A to B & D together is 1 : 2. Find how many days A worked?
(a) 7days
(b) 5days
(c) 8days
(d) 4days
(e) 9 days
Q2. A and D starts working together, but A worked with 50% of his efficiency. C starts working with 66 ⅔% more of his efficiency on an another work which is 62 ½ % of the work which A and D were doing. Find the ratio of days taken by C to days taken by A and D together to complete the work?
(a)5:3
(b)5:7
(c)3:5
(d)3:7
(e)3: 11
Q3. D started the work and left it after working for X days and then C joined the work and worked for Y days. After C left, E completed the remaining work in 3 days. Find number of days for which D and C worked individually, given that value of Y is 200% of value of X?
(a) 6 days & 12 days
(b) 8 days & 16 days
(c) 7 days & 14 days
(d) 9 days & 18 days
(e) 5 days & 10 days
Q5. Three persons B, D and F starts working together. If B works with 75% of his efficiency and D worked 25% more efficiently. All three get 27180 Rs. as total wages. Find the individually wage of all according to work done by them (in Rs.)?
(a) 6795, 6795 & 13590
(b)7695, 7695, &13590
(c)6595, 6595, & 14590
(d) 7965, 6795, & 12590
(e) None of these
Direction (6-10): – Line chart given below shows time taken by five different persons to complete a work ‘M’ alone. Ratio of efficiency of all five persons remain same throughout any work. Study the data carefully and answer the following questions.
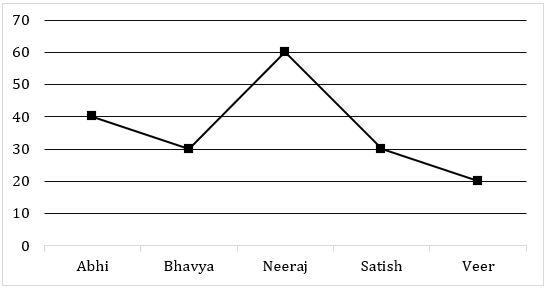
Q6. All five starts working together to complete work ‘X’. ‘Veer’ left after 8 days. Work done by ‘Bhavya’ is same as work done by ‘Neeraj’ while ‘Abhi’ and ‘Neeraj’ worked for same time. ‘Satish’ worked for ‘y’ days. If ‘Bhavya’, ‘Neeraj’ and ‘Satish’ together can complete work ‘X’ in 24 days then find the value of ‘y’ if Bhavya worked for starting 10 days.
(a) 7 days
(b) 9 days
(c) 11 days
(d) 13 days
(e) 15 days
Q7. Abhi and Neeraj together can complete work ‘Z’ in (A + 42) days while Bhavya and Satish together can complete work ‘Z’ in (A + 15) days. All start the work Z such that ratio between work done by Abhi, Bhavya and Veer is 1 : 2 : 3, while ratio between days, Neeraj, Satish and Veer worked is 2 : 2 : 1. Find how many days ‘Bhavya’ worked.
(a) 10 days
(b) 15 days
(c) 20 days
(d) 30 days
(e) 40 days
Q8. All five persons started together to complete work ‘Y’. Veer worked for starting 6 days and left the work. After 3 days more both Bhavya and Satish left too. Remaining 40% work should be completed by Abhi and Neeraj together but ‘Abhi’ left after ‘x’ days. Remaining work is completed by ‘Neeraj’ in ‘z’ days. If ‘z – x = 3’, then number of days for which ‘Neeraj’ worked is what percent more than number of days for which ‘Abhi’ worked.
(a) 33⅓%
(b) 50%
(c) 66⅔%
(d) 75%
(e) 100%
Q9. Abhi, Bhavya and Neeraj together starts to do work ‘M’. After 7 days ‘Neeraj’ left and after 3 days more ‘Abhi’ and ‘Bhavya’ left. Remaining work is completed by Satish and Veer working alternatively in ‘y’ days. If ‘y’ is integer then find ‘Veer’ worked for how many days?
(a) 3 days
(b) 4 days
(c) 5 days
(d) 6 days
(e) Cannot be determined
Q10. Abhi, Bhavya and Satish starts working together to complete work ‘M’. After 5 days, Bhavya and Satish replaced by Neeraj and Veer. After 5 more days Abhi left the work. After 1 more day Veer left too. Neeraj worked for total ‘x’ days. In other case Abhi and Bhavya starts working together to complete ‘M’. After 4 days both are replaced by Veer. Veer worked for 5 days and replaced by Satish who worked for 8 days. Remaining work is completed by Neeraj in ‘y’ days. Find (y-x)²?
(a) 25
(b) 36
(c) 49
(d) 64
(e) 81
Solutions
Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Foun...
