Q1. (x-2)! blue balls and (x-1)! white balls are there in the bag. If one ball is drawn at random from the bag then the probability that the drawn ball is blue is 1/90. Find total number of white balls in the bag. (!-factorial)
(a) 84 !
(b) 86 !
(c) 87 !
(d) 89 !
(e) 88 !
Q2. A bag contains 50 balls in which there are 20 white balls and some red and yellow balls. If three balls are picked up from the bag without replacement, then the probability of the first ball being white, second being red and third being yellow is 4/105. Find the number of yellow balls in the bag.
(a) 16
(b) 12
(c) 10
(d) 14
(e) either (a) or (d)
Q3. Diagonal of a square is equal to diameter of a circle. Area of circle is 1232 sq.cm. A cube is formed using the square as face of cube. This cube is melted and recast to form a cylinder of radius 28 cm. find height of cylinder thus formed. (approx.)
(a) 9 cm
(b) 12 cm
(c) 7 cm
(d) 14 cm
(e) 17 cm
Q4. An ice cream box full of ice cream is in the form of cuboid, having 54cm breadth, 30cm height and 77cm length. Ice cream from the cuboidal box is served in the cone. Radius of cone is 425% more than its height. If ratio of height of the cone to cuboid is 1 : 5, then find the number of cones required to serve the full quantity of ice cream of cuboidal box.
(a) 25
(b) 10
(c) 30
(d) 15
(e) 20
Q5. The ratio between the radius of two hemispherical solid tin pieces is 2 : 3 and difference between volumes of both of the the pieces is 6688/21 cm3. These two hemispheres are melted and recast into a cylindrical vessel and used 592/3 π cm3 extra tin material for polishing the vessel. If ratio between height & radius of cylindrical vessel is 3 : 4, then find the total surface area of cylindrical vessel?
(a) 724 cm²
(b) 176 cm²
(c) 704 cm²
(d) 744 cm²
(e) None of these
Q6. A solid spherical vessel of radius 63cm is full of water. Water from the spherical vessel is emptied completely into X number of cylindrical vessel and Y number of hemispherical vessels. Radius of hemispherical vessel and cylindrical vessel is same and radius of spherical vessel is 200% more than that of hemispherical vessel. If height of cylindrical vessel is 10cm, then which of the following is the possible value of (X, Y).
(I) (20, 42)
(II) (35, 29)
(III) (16, 51)
(IV) (21, 39)
(V) (30, 32)
(a) Only III
(b) Only I & II
(c) Only IV & I
(d) Only I, II & V
(e) None of the above.
Q7. Tejas can cross a pole in 6 sec and a 360 m long platform in 15 sec. If Tejas can cross another train running in same direction at speed of 72km/hr in 20 sec, then find time taken by another train to cross that platform?
(a) 24 sec
(b) 26 sec
(c) 28 sec
(d) 30 sec
(e) 27.5 sec
Q8. Train – Y crosses Train – X while running in same direction in 120 seconds and Train – Y crosses Train – X in 40/3 seconds while running in opposite direction. If Train – X is running at 120 km/hr, then find speed of Train – Y (in km/hr).
(a) 150
(b) 180
(c) 200
(d) 160
(e) None of the above.
Q9. Train – B crosses train – A running in same direction in 105 seconds and train – A crosses a man running in same direction in 20 seconds. Train – B crosses a 600m long platform in 20 seconds. If ratio of length of train – A to that of train – B is 5 : 2 and speed of man is 25% of that of train – A, then find speed of train – B.
(a) 144 km/hr.
(b) 180 km/hr.
(c) 162 km/hr.
(d) 114 km/hr.
(e) 150 km/hr.
Q10. Length of train A is 75% more than that of train B and both trains cross each other running in opposite direction in 44/5 sec. If three compartments (length of each compartment is 20 meters) are added in train B, then both trains cross each other running in opposite direction in 10 sec. Find difference between speed of train A & speed of train B? (in meter/sec)
(a) 10
(b) 12
(c) 16
(d) 20
(e) Can’t determined
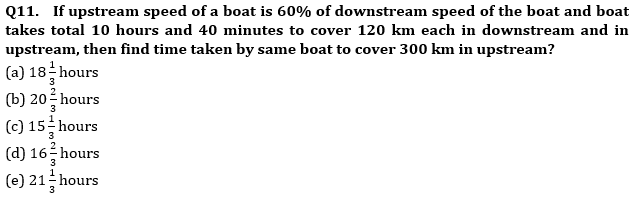
Q12. Ratio between speed of boat in still water to downstream speed is 3 : 4 and boat takes 1 hour 40 minutes more to cover 80 km in still water than in downstream. Find time taken by boat to cover distance of 36 km in upstream?
(a) 4.5 hours
(b) 5.5 hours
(c) 3.5 hours
(d) 2.5 hours
(e) 1.5 hours
Q13. A man can row the boat in downstream from point A to C in 16 hours. But he return from point B, which is exactly mid-point of A and C to upstream in 12 hours. Find the ratio of speed of stream to the speed of man in still water ?
(a) 1 : 5
(b) 2 : 3
(c) 3 : 2
(d) 4 : 3
(e) 5 : 3

Q15. Ratio of speed of boat in upstream to that of in downstream is 2:x and distance travelled by boat in still water in 4hr is equal to distance travelled by boat in upstream in 5hr. Then find value of ‘x’?
(a) 7
(b) 3
(c) 5
(d) None of these
(e) Can’t be determined
Solutions

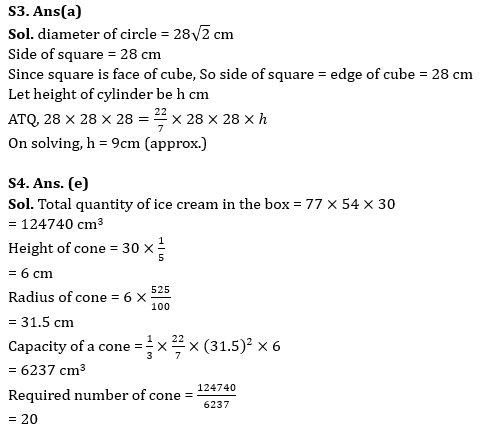






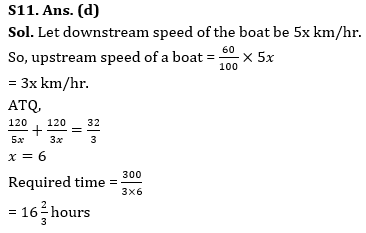







 Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Main...
 Quantitative Aptitude Quiz For Bank Foun...
Quantitative Aptitude Quiz For Bank Foun...


