Q1. A sum of money invested at simple interest doubles itself in 3 yrs and 4 months. Find in how many years it will become 7 times of itself at the same rate? (in years)
(a) 20
(b) 18
(c) 15
(d) 21
(e)24
Q2. Sohail invested Rs. 5000 in a scheme offering 10% simple interest. If the same sum is invested in another scheme for 2 more years offering 15% simple interest then it would have fetched Rs. 2000 more. Find time period (in years) of investment in first scheme.
(a) 2.5
(b) 4
(c) 3
(d) 1.5
(e) 2
Q3. A man invested Rs. 1600 on CI for two years at the rate of R% p.a. and gets amount of Rs. 2304. If man invested same sum on SI for same period of time at the rate of (R – 8)%, then find interest he will get?
(a) 384 Rs.
(b) 324 Rs.
(c) 316 Rs.
(d) 372 Rs.
(e) 306 Rs.
Q4. A certain amount was invested for certain time and at a certain rate at simple interest. After 2 years, amount obtained is Rs.24000 and after 5 years total amount obtained Rs.30000. Find the amount invested initially.
(a) Rs.25000
(b) Rs.20000
(c) Rs.40000
(d) Rs.30000
(e) Rs.35000
Q5. Anurag borrowed a sum of Rs.15000 from two banks at SI. If both banks charged interest at 12% p.a. and at 20% p.a. and Anurag paid Rs.2560 as total interest after completion of 1 year, then find amount borrowed by him at 20% p.a.
(a) Rs.7500
(b) Rs.8000
(c) Rs.5500
(d) Rs.7000
(e) Rs.9500
Q6. If simple interest on a certain sum of money for three years is Rs. 450 and the compound interest on the same sum at the same rate for 2 years is Rs. 309, then the principal invested in rupees is :
(a) Rs. 3000
(b) Rs. 1875
(c) Rs. 1500
(d) Rs. 2250
(e) Rs. 2500
Q7. An amount becomes Rs. 12375 in two years and Rs. 27843.75 in 4 years at C.I., then find the Amount.
(a) Rs. 5000
(b) Rs. 5500
(c) Rs. 6000
(d) Rs. 6500
(e) Rs. 4500
Q8. Compound interest on certain sum for 2 years is Rs 1782. And simple interest at same interest on same sum is Rs 1620 in 2 years. Find the sum.
(a) Rs 5500
(b) Rs 4500
(c) Rs 4050
(d) Rs 5025
(e) Rs 4000
Q9. If difference between S.I on Rs. 2000 and C.I on 1600 for two year at same rate of interest is Rs. 64. Find rate of interest. (S.I > C.I)
(a) 5%
(b) 10%
(c) 20%
(d) 8.5%
(e) 12.5%
Q10. Arun invested Rs. 10,000 for three years at CI at the rate of 20% per annum. If in 1st and 3rd year interest is calculated annually and in 2nd year it was calculated half-yearly, then find the total interest received by Arun in three years?
(a) Rs 7554
(b) Rs 7424
(c) Rs 7868
(d) Rs 7262
(e) Rs 7343
Q11.Difference between CI received in first 1.5 years (compounded annually) at 20% per annum and CI received in last 1.5 years when compounded half yearly at the same rate of interest on the same sum is Rs 715 then find the sum?
(a) Rs. 66,000
(b) Rs. 65,000
(c) Rs. 64,500
(d) Rs. 65,500
(e) Rs. 67,500
Q12. Deepak invested some amount on SI out of Rs.47000 and rest amount on C.I. for two years. If S.I. is offering 12% p.a. and C. I. is offering 15% p.a. compounding annually and C.I. is Rs.532.5 more than S.I., then find amount invested by Deepak on C.I?
(a) Rs.23000
(b) Rs.22000
(c) Rs.21000
(d) Rs.25000
(e) Rs.24000
Q13. Dharam invested Rs.10000 in two schemes for two years and both schemes offer R% S.I. If difference between S.I. earned on both schemes is Rs.480 and ratio of interest earned from both schemes is 3 : 2. Then, find the value of R.
(a) 15 %
(b) 10 %
(c) 20 %
(d) 16 %
(e) 12%
Q14. Amount of Rs. 8000 is lent at simple interest in two parts at 20% and 10% respectively. If after one year he will get Rs. 1150 as interest then find amount which was lent at 20% per annum.
(a) Rs.3000
(b) Rs.5000
(c) Rs.3500
(d) Rs.4500
(e) Rs. 4200
Q15. A lent B Rs.12000 on C.I. at the rate of 20% per annum and at the end of first year B borrowed Rs. ‘x’ more from A on C.I. at the same rate. If at the end of second year, B paid total amount of Rs.20400 to A, then find value of x?
(a) Rs.2400
(b) Rs.2000
(c) Rs.3600
(d) Rs.2600
(e) Rs.4000
Solutions
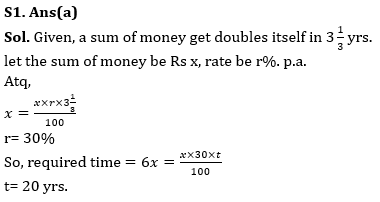


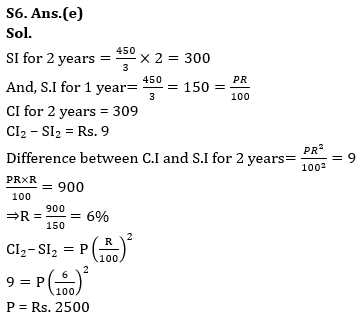



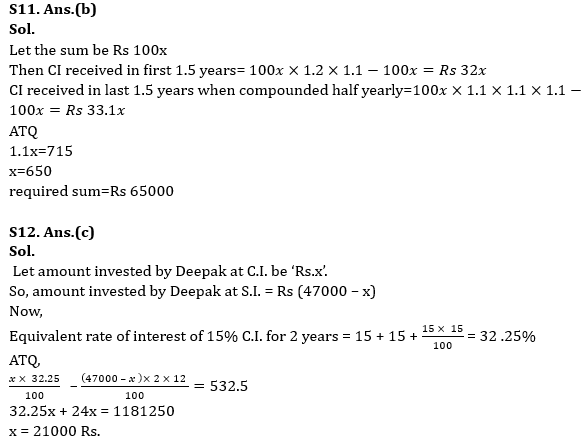







 Quantitative Aptitude Quiz For Bank Main...
Quantitative Aptitude Quiz For Bank Main...
 Quantitative Aptitude Quiz For Bank Foun...
Quantitative Aptitude Quiz For Bank Foun...


