Union Bank SO Practice Set- Quant (With Answers)

Quantitative Aptitude is one of the most critical sections in the Union Bank Specialist Officer (SO) recruitment exam. It not only evaluates a candidate’s numerical ability but also assesses logical reasoning through numbers, data interpretation and real-life application of mathematical principles. For aspirants aiming to excel in the exam, practising quant problems regularly is crucial to improve both accuracy and speed. This Union Bank SO Quant Practice Set is specifically designed to help you reinforce core concepts and get exam-ready.

Union Bank SO Quantitative Aptitude

The questions in the quantitative section are known to be moderately difficult, requiring a solid understanding of arithmetic, algebra, number systems, percentages, profit and loss, ratio and proportion, time and work, time-speed-distance, averages, and data interpretation. Given the time constraints in the actual exam, it’s not just about solving problems, it’s about solving them fast and correctly. That’s where this practice set proves valuable. This Quantitative Aptitude practice set mirrors the pattern and difficulty level of Union Bank SO 2025 exams.

Union Bank SO Practice Set- Quant (With Answers)

Directions (1-3): In the given questions, two quantities are given, one as ‘Quantity I’ and another as ‘Quantity II’. You have to determine relationship between two quantities and choose the appropriate option

Q1. Quantity I. The perimeter of an equilateral triangle having height 12 cm and area 36 cm2.

Quantity II. Three years ago, the Sum of age of Babita and Savita was 24 years. Babita is 8 years older than Savita. Find the present age of Savita. 

(a) Quantity I > Quantity II 

(b) Quantity I < Quantity II

(c) Quantity I ≥ Quantity II 

(d) Quantity I ≤ Quantity II 

(e) Quantity I = Quantity II or no relation

Q2. Quantity I. Speed of the train (in m/sec.) having length 360 m which crosses a pole in 15 seconds.

Quantity II. Speed of the boat in still water (in kmph) which covers 240 km in 8 hours in downstream when the speed of current is 6kmph.

(a) Quantity I > Quantity II 

(b) Quantity I < Quantity II

(c) Quantity I ≥ Quantity II 

(d) Quantity I ≤ Quantity II 

(e) Quantity I = Quantity II or no relation

Q3. Quantity I. Maximum possible difference between two natural numbers having an average of 30

Quantity II. Value of x. 

20% × x + 1623 % of 96 = 25

(a) Quantity I > Quantity II 

(b) Quantity I < Quantity II

(c) Quantity I ≥ Quantity II 

(d) Quantity I ≤ Quantity II 

(e) Quantity I = Quantity II or no relation

Q4. The cost of ploughing a square park at the rate of Rs 85 per square meter is Rs 3060. Find the cost (in Rs) of fencing the park at the rate of Rs 20 per meter. 

(a) 420

(b) 400

(c) 440

(d) 460

(e) 480

Q5. There are three numbers A, B and C. The ratio of A to B is 2 : 5 while the ratio of B to C is 4 : 7. If the difference between A and C is 81 then find the average of the numbers.

(a) 60

(b) 69

(c) 54

(d) 57

(e) 63

Directions (6-10): What approximate value will come in place of question mark (?) in the following questions (You are not expected to calculate the exact value).

Q6. (14.85)2 × 4.75 + (45.02)2 × 3.99 = ?

(a) 9235

(b) 9245

(c) 9225

(d) 9255

(e) None of these

Q7. 239.96 × 6.21 – 124.57 × 1.83 =?

(a) 1190

(b) 1180

(c) 1170

(d) 1160

(e) 1150

Q8. (19.87)2 – 725.29 ÷ 24.99 = ? × 2 – 75.89

(a) 225.5

(b) 226.5

(c) 228.5

(d) 223.5

(e) 229.5

Q9. (4.96 × 5.03-2) ÷ (4.99-6)= 5?

(a) 9

(b) 8

(c) 7

(d) 6

(e) 10

Q10. (3/8) of 816 + 12.5 % of 32.11 = (?)2 + 84.92

(a) 15

(b) 12

(c) 11

(d) 10

(e) None of these

Direction (11-15): The Bar graph given below shows the total number of trees planted by five different schools (P, Q, R, S and T) and number of trees of type A and Type B planted by these schools. Read the data carefully and answer the questions.

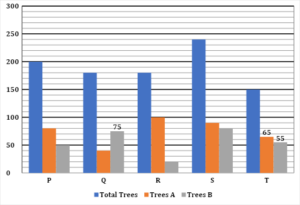
Note: Total number of trees planted by any school = Type A trees + Type B trees + Type C trees

Q11. Which school planted maximum number of type C trees.

(a) P

(b) Q

(c) R

(d) S

(e) Both P and S

Q12. Total type C trees planted by schools R, S and T together are how many more or less than total type A trees planted by schools P, Q and R together.

(a) 40

(b) 45

(c) 55

(d) 60

(e) 50

Q13. If the total trees planted by school X is 20% more than that of by school S, then find the number of type C types trees planted by school X, given that the ratio of type A, B and C trees planted by school X is 5: 6: 7.

(a) 118

(b) 116

(c) 120

(d) 115

(e) 112

Q14. Find the ratio of total type A trees planted by schools P and R together to type C trees planted by school S and T.

(a) 8 : 9

(b) 7: 8

(c) 5: 7

(d) 9 : 5

(e) None of these

Q15. Find the average of C type trees planted by all the schools.

(a) 55

(b) 57

(c) 58

(d) 59

(e) 51

Q16. A sum of Rs 4000 fetches an interest of Rs 1280 at x% p.a. on simple interest in four years. Find the compound interest (in Rs.) obtained on Rs. 7000 at the rate of (x + 12) % p.a. in two years. 

(a) 2040

(b) 3080

(c) 5050

(d) 6040

(e) 2080

Q17. The distance between two points P and Q is 440 km. Car A starts from point P at 9 am at a speed of 55 kmph while car B starts from point Q at 11am with a speed of 45kmph. Moreover, Car A increases its speed at 12 noon by 15kmph. At what time will they meet if they travel at a constant speed.

(a) 2 pm

(b) 3 pm

(c) 4 pm

(d) 5 pm

(e) 6 pm

Q18. A, B and C can complete a work in 20 days, 30 days and 40 days respectively. All started the work together but B and C left the work 10 days before completion of the work. In how many days the whole work was finished.

(a) 5 days

(b) 10 days

(c) 161/13  days

(d) 178/13 days

(e) 190/13 days

Q19. How many kg of type A sugar costing Rs 20 per kg is mixed with 10kg of type B sugar costing Rs 30 per kg so that by selling the mixture at Rs 36 per kg there will be a profit of 50%.

(a) 20

(b) 10

(c) 15

(d) 25

(e) None of these

Q20. A and B started a business by investing Rs 7200 and Rs 8400 respectively. There was a condition that at the end of the year only 50% of the profit will be divided as per their investment and the rest 50% will be equally divided. If A received Rs 3900 as his profit then find the total profit (in Rs).

(a) 8112

(b) 7878

(c) 9100

(d) 7308

(e) 8188

Q21. When Ankit was born his father was 32 years old. Brother of Ankit is twice his present age. Average age of his brother and his sister is 14 years. If present age of his father is 40 years, then find the present age of his sister (in years).

(a) 10

(b) 12

(c) 8

(d) 6

(e) None of these

Q22. A man sold a bat for Rs 1000 and made 25% profit. At what loss % should he sell a ball worth Rs 400 so that net profit becomes zero.

(a) 20

(b) 25

(c) 30

(d) 35

(e) 50

Q23. The average age of 28 students in a class is 28 years. If the youngest and the oldest students are excluded then still the average age of the class remains the same. Find the age (in years) of the oldest student if the ratio of the oldest student to the youngest student is 4: 3.

(a) 32

(b) 36

(c) 28

(d) 40

(e) 44

Q24. A vessel contains 208 Liters mixture of milk and water in the ratio 7:6. If 52 Liters mixture is taken out and x litres water is added into the remaining mixture, then the ratio of milk to water becomes 6:7. Find the value of x. 

(a) 22

(b) 24

(c) 20

(d) 18

(e) 26

Q25. Speed of boat in upstream is half of the speed of the boat in downstream. If the boat covers 64 km upstream and the same distance downstream in 24 hours. Find the distance travelled by the boat in 4 hours in still water.

(a) 24

(b) 28

(c) 20

(d) 32

(e) 36

Directions (26-30): In each of these questions a number series is given. In each series only one number is wrong. Find out the wrong number.

Q26.  7, 8, 10, 15, 40, 160, 880

(a) 40

(b) 10

(c) 8

(d) 7

(e) 15

Q27. 480,     300,     720,     180,     900,     150, 1050  

(a) 480

(b) 180

(c) 900

(d) 300

(e) 150

Q28. 20, 33, 51, 81, 118, 161 214

(a) 161

(b) 81

(c) 33

(d) 20

(e) 51

Q29. 667,  395, 259, 192, 157, 140,  131.5

(a) 667

(b) 395

(c) 192

(d) 157

(e) 140

Q30. 4,  5, 11, 47, 264,1559, 9335

(a) 264

(b) 5

(c) 11

(d) 57

(e) None of these

Directions (31-35): The given pie chart shows percentage distribution of the customers visited in five different saloons (A, B, C, D and E) on Sunday and the table shows the ratio of the customers who went for hair cutting, massage and shaving in the respective saloons.

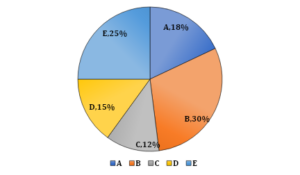
Note: The difference between the number of customers in saloon A and C is 150

Saloons	Ratio of the customers who went for hair cut to massage to shaving
A	2:3:4
B	4:5:6
C	5:10:15
D	3:4:8
E	7:8:10

Q31. Find the ratio of the customers who went for shaving in Saloon C to the customers who went for massage in Saloon D.

(a) 3: 2

(b) 2: 3

(c) 3: 5

(d) 4: 5

(e) 5: 6

Q32. The customers who went to Saloon D for shaving and massage together is how many more or less than the customers who went for haircut in Saloons C and D together.

(a) 125

(b) 150

(c) 175

(d) 225

(e) 250

Q33. The customers who went for shaving in Saloons D and E together are how much percent more or less than those who went for haircut in Saloons B and D together.

(a) 64 7/11%

(b) 65 7/11%

(c) 63 3/11%

(d) 63 7/11%

(e) None of these

Q34. Find the ratio of the customers who went for massage in Saloons A and C together to those who went for haircut in the same saloons.

(a) 5: 8

(b) 5: 9

(c) 15: 13

(d) 5: 3

(e) None of these

Q35. If in Saloon X, the number of customers who went for shaving, massage and haircut are 10%,20% and 20% more than those who went in Saloon A respectively, then find the total number of customers who visited Saloon X.

(a) 320

(b) 420

(c) 660

(d) 550

(e) 520

Solutions

S1. Ans.(a)

Sol. Quantity I. 

Area of triangle = 36 cm2

12 × base × height = 36

12 × base × 12 = 36

Base = 6 cm

Perimeter = 3 × 6 = 18 cm

Quantity II.

Let the present age of Babita be b years and that of Savita be s years.

b + s = 24 + 3 + 3

b + s = 30 ……….(i)

b – s = 8 ………….(ii)

From (i) & (ii)

s = 11 years 

S2. Ans.(e)

Sol. Quantity I. Required speed = 360/15  = 24 m/s

Quantity II. Downstream speed =  240/8 = 30kmph

Let the speed of boat in still water be s kmph

s + 6 = 30

s = 24kmph

S3. Ans.(a)

Sol. Quantity I. Average of two numbers = 30

Sum = 60

Let the smallest number be x = 1

Highest number be y = 60 – x = 59

Required difference = 58

Quantity II.

20% × x + 1623 % of 96 = 25

x = 45

S4. Ans.(e)

Sol. Area of the park = 3060/85 = 36 m2

Side = 6 meters

Perimeter of the park = 4 × 6 = 24 m

Required cost = 24 × 20 = Rs 480

S5. Ans.(e)

Sol. A : B  = 2 : 5 

B  : C  = 4  : 7

A : B : C = 8 : 20 : 35

Let A, B and C be 8x, 20x and 35x respectively

ATQ,

35x – 8x =81

27x = 81

x = 3

A = 8x = 24

B = 20x = 60

C = 35x = 105

Required average = (24+60+105)/3 = 63

S6. Ans.(c)

Sol. 152 × 5 + 2025 × 4 =?

1125+ 8100 =?

? = 9225

S7. Ans.(a)

Sol. 240 x 6 – 125 x 2 =?

1440 – 250= ?

? = 1190

S8. Ans.(d)

Sol. (20)2 – 725 ÷ 25 = ? × 2 – 76

400 – 29 = ? × 2 – 76

? = 223.5

S9. Ans.(e)

Sol. (56 × 5-2) ÷ (5-6) = 5?

54 ÷ (5-6) = 5?

? = 4 + 6

? = 10

S10. Ans.(a)

Sol. (3/8) of 816 + 12.48 % of 32.11 = (?)2 + 84.92

306 + 4 – 85 = (?)2

?2 = 225

? = 15

Solutions (11–15): 

Schools	Total trees	Type A trees	Type B trees	Type C trees
P	200	80	50	200 – (80+50) =70
Q	180	40	75	180–40+75= 65
R	180	100	20	180 –100+20= 60
S	240	90	80	240–90+80=70
T	150	65	55	150–65+55=30

S11. Ans.(e)

Sol. Both School P and S planted 70 type C trees

S12. Ans.(d)

Sol. Required difference = (80 + 40 + 100) – (60+ 70 + 30) = 60

S13. Ans.(e)

Sol. Total trees planted by school X = 120% of 240 = 288

Type C trees planted by school X = 7/18 of 288 = 112

S14. Ans.(d)

Sol. Required Ratio = 180/100 = 9:5

S15. Ans.(d)

Sol. Required average = (70+65+60+70+30)/5 = 59

S16. Ans.(b)

Sol. ATQ, (4000  x  ×4 )/ 100 = 1280

x = 8%

for compound interest rate is (x + 12) % = 20%

Equivalent rate of interest at 20% p.a. for 2 years = (20 + 20 + 20  ×20  100)% = 44%

Required interest = 44/100x7000 = Rs 3080

S17. Ans.(a)

Sol. At 12 noon,

Distance travelled by car A = 55 3 = 165 km

Distance travelled by car B = 45 ×1 = 45km

Distance between them = 440 –(165 + 45)= 230 km

Required time = 230/(70+45) = 2 hours

So, they will meet at 2pm.

S18. Ans.(e)

Sol. Let the total work be 120 units (LCM of 20, 30 & 40) and total time in which whole work was finished be ‘’t’’ days

Efficiency of A = 120/ 20 = 6 units per day

Efficiency of B = 120/ 30 = 4 units per day

Efficiency of C = 120/ 40 = 3 units per day

Work done by A = 6t units

Work done by B = 4(t – 10) units

Work done by C = 3(t – 10) units

6t + 4(t-10) + 3(t-10) = 120 

6t + 4t – 40 + 3t – 30 = 190

13 t = 190

t = 190/13 days

S19. Ans.(c)

Sol. CP of the mixture = 36 ×100/150 = Rs 24 per kg

Using allegation,

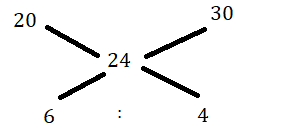
Ratio = 6: 4 = 3 : 2

2 units 🡪 10 kgs

3 units 🡪 15kgs

S20. Ans.(a)

Sol. Let the total profit be Rs 4x

Ratio of profit share of A and B is 6:7

Net profit of A = x + 6/13 × 2x = 3900

(25/13)  x = 3900

x = 2028

4x = 8112

S21. Ans.(b)

Sol. Present age of his father = 40 years

Present age of Ankit = 40-32 = 8 years

Present age of his brother = 16 years

Sum of present ages of his brother and his sister = 14  × 2 = 28 years

Age of his sister = 28 – 16 = 12 years

S22. Ans.(e)

Sol. Cost price of the bat = 100/125 × 1000 = Rs 800

Profit= 1000 – 800 =Rs 200

For net profit to be zero there should be loss of Rs 200 on selling the ball

Loss % = 200/400 × 100 = 50 %

S23. Ans.(a)

Sol. If the youngest student and the oldest student are removed the average remains the same it means average age of the youngest and the oldest student is same i.e., 28 years

Let the age of the oldest student be 4x then the age of the youngest student will be 3x

4x + 3x = 56

x = 8

4x = 32years

S24. Ans.(e)

Sol. Initial quantity of milk = 7/13 × 208 = 112 liters

Initial quantity of water = 208 – 112 = 96 liters

Quantity of milk removed = 7/13 × 52 = 28 liters

Quantity of water removed = 52- 28 = 24 liters

ATQ,

(112-28)/(96-24+x) = 67

x = 26

S25. Ans.(a)

Sol. Let the upstream speed be 2x and downstream speed be x

ATQ,

64/x + 64/2x = 24

x = 4 kmph

2x = 8kmph

Speed of boat in still water = 4+82 = 6kmph

Required distance = 6 × 4 = 24 km

S26. Ans.(e)

Sol. The wrong number is 15.

Pattern of the series

S27. Ans.(d)

Sol. Wrong number = 300

Pattern of series – 

S28. Ans.(e)

Sol. The wrong number is 51.

Pattern of the series

Difference should be alternate prime numbers

S29. Ans.(c)

Sol. The wrong number is 192.

Pattern of the series

667 – 272 = 395

395 – 136 = 259

259 – 68 = 191

191 – 34 = 157

157 – 17 = 140

140 – 8.5 = 131.5

S30. Ans.(a)

Sol. The wrong number is 264

Pattern of the series

4 + 60 = 5

5 + 61 = 11

11 + 62 = 47

47 + 63 = 263

263 + 64 = 1559

1559 + 65 = 9335

Solutions (31–35):

Let the total number of customers on Sunday be 100x

ATQ

18x – 12x = 150

6x = 150

x = 25

Customers of shop A = 18x = 450

Customers of shop B = 30x = 750

Customers of shop C = 12x = 300

Customers of shop D = 15x = 375

Customers of shop E = 25x = 625

Let the number of customers who went to saloon A for haircut, massage and shaving be 2a , 3a and 4a respectively.

2a + 3a + 4a = 450

a = 50

2a = 100

3a = 150

4a = 200

Similarly for other saloons

SALOONS	Number of customers	Customers for Haircut	Customers for Massage	Customers for Shaving
A	450	100	150	200
B	750	200	250	300
C	300	50	100	150
D	375	75	100	200
E	625	175	200	250

S31. Ans.(a)

Sol. Required ratio = 150/100 = 3/2 = 3: 2

S32. Ans.(c)

Sol. Required difference = (100 + 200) – (50 + 75) = 175

S33. Ans.(d)

Sol. Required percentage = [(200+250)-(200+75)]/275 × 100 = 63 7/11%

S34. Ans.(d)

Sol. Required ratio = (150+100)/(100+50) = 250/150 = 5: 3

S35. Ans.(e)

Sol. Required sum = 200 ×  11/10 + 150 ×  12/10 + 100 ×  12/10 = 220 + 180 + 120 = 520

Related Posts
Union Bank SO Practice Set- Reasoning (With Answers)
Union Bank SO Syllabus	Union Bank SO Salary
Union Bank SO Previous Year Question Papers