Directions (1-5): The following table shows different plans offered by a lender, type of interest and rates of interest applicable during first, second and third years.
(Note: Some values are missing, you need to calculate those values if required.)
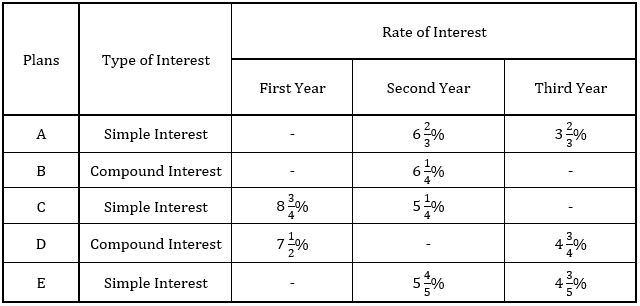
Q1. If two persons borrows an equal amount of Rs.12000 under plan B and plan E respectively and rate of interest for the first year under plan B and D is same, then what is the difference between second year’s interests alone paid by each of them?
(a) Rs.105.25
(b) Rs.110.25
(c) Rs.115.25
(d) Rs.120.25
(e) Cannot be determined
Q2. A person borrows Rs.20480 under plan C. After completion of the loan tenure of three years under plan C, he extends the tenure for further two years under plan D on the amount payable at that time. He settles his loan by paying Rs.27778. What is the rate of interest for the second year under plan D if rate of interest for the third year under plan C and D is same?
(a) 5 ¾ %
(b) 5 ¼ %
(c) 6 ¼ %
(d) 4 ¾ %
(e) 6 ¾ %
Q3. If the amounts borrowed by a person under plan B and C are in the ratio 16 : 13 and rate of interest applicable during the first year under plan B and D is same, then what is ratio of interests payable under these plans at the end of second year.
(a) 5 : 6
(b) 3 : 5
(c) 3 : 4
(d) 5 : 4
(e) None of these
Q4. The lender decides to offer a fixed rate of interest at 6⅔% per year under plan C. By how much percent the interest payable will increase from the interest payable previously under the old plan for the period of three years if rate of interest for the third year under old plan C and plan D is same?
(a) 6⅓%
(b) 6 ¼ %
(c) 6⅔%
(d) 6⅖%
(e) Cannot be determined
Q5. Rates of interest for the first year under plan A and E are 8⅔% and 7⅗% respectively. A person borrows a total of Rs.30000 partially under plan A and E and pays a total interest of Rs.5540 at the end of third year. How much amount does he borrow under plan A?
(a) Rs.14000
(b) Rs.18000
(c) Rs.16000
(d) Rs.12000
(e) Rs.20000
Directions (6-10): A new party XYZ, participated in election in 5 constituencies (A, B, C, D & E). Pie chart shows % distribution of party’s total votes scored by its 5 candidates and line graph shows, % of votes scored by winner candidates out of total votes polled in these 5 constituencies.
Note: All the votes must be calculated in nearest hundreds.
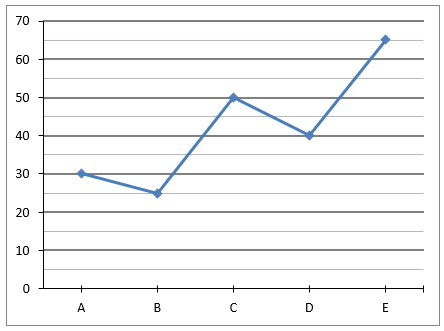
Q6. Candidate of party XYZ is winner from constituency B and defeated runner-up candidate by 7000 votes. None of the candidates from this constituency obtained vote less than 12000, then calculate maximum possible number of candidates from constituency B.
(a) 6
(b) 7
(c) 15
(d) 13
(e) can’t be determined
Q7. Party XYZ wins from constituency C. In constituency E total votes polled are 45000 less than that of constituency C. Find from how many votes the candidate of party XYZ lost in constituency E?
(a) 79500
(b) 91500
(c) 26500
(d) 27000
(e) 0
Q8. Out of constituency A and D, one of the seats was won by party XYZ. In lost constituency their candidate was runner up by 15000 votes. Find maximum possible difference between total votes polled in both of these constituencies.
(a) 50000
(b) 37500
(c) 25000
(d) either (A) or (B)
(e) either (B) or (C)
Q9. In constituencies A & E, both candidates of party XYZ are runner up, and lost by same number of votes. If the votes polled in E is 180000, find approximate number of votes polled in constituency A.
(a) 350000
(b) 365000
(c) 180000
(d) 100000
(e) None of these
Q10. Which of the following condition is never possible?
(i) constituency B and C have equal number of votes polled given that party wins from C.
(ii) candidate of party XYZ lost by 28000 voters from constituency E.
(iii) constituency A and B have equal number of votes polled.
(iv) winner candidate of constituencies B and D got equal number of votes.
(a) only (i)
(b) Only (i) and (iii)
(c) (i), (ii) and (iv)
(d) (i) and (ii)
(e) All of these are possible
Solutions
Data Interpretation Questions for SBI PO...
Data Interpretation Questions For Bank E...
Quantitative Aptitude Quiz For Bank Main...
