Reasoning Ability Quiz For SBI, IBPS Prelims 2021- 9th March

Table of Contents

Directions (1-5): In each of the questions below are given some statements followed by some Conclusions. You have to take the given statements to be true even, if they seem to be at variance from commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts.
(a) If both conclusions I and II follow.
(b) If either conclusion I or II follows.
(c) If neither conclusion I nor II follows.
(d) If only conclusion II follows.
(e) If only conclusion I follows.

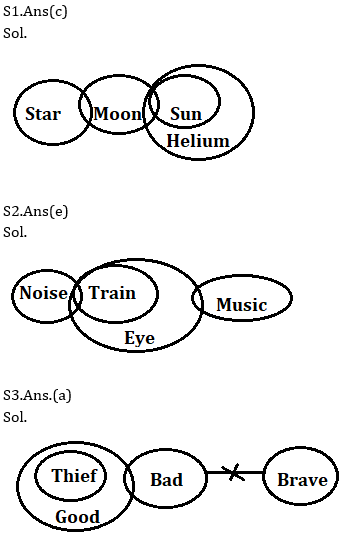
Q1. Statements:
Some Star are moon
Some moon are sun
All sun is Helium
Conclusion:
I: Some star are helium
II: All sun can never be star

Q2. Statements:
Only a few Noise are Train
All Train are Eye
Only a few Eye are Music
Conclusion:
I: All Music can be Train
II: No Noise is music

Q3. Statements:
All Thief are Good
Only a few Good are bad
No bad is Brave
Conclusions:
I. Some Good are not Brave
II. All Thief can be Bad

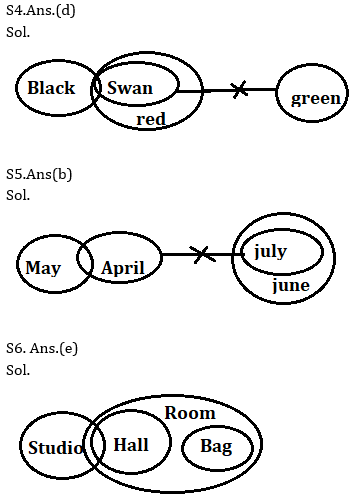
Q4. Statements:
Some black are swan
All swan are red
No swan are green
Conclusions:
I. All green can never be red
II. Some black are not green

Q5. Statements:
Some May are April
No April is July
All July are June
Conclusions:
I: Some May are June
II: No June is May

Directions (6-10): In each of the questions given below some statements are followed by some conclusions. You have to take the given statements to be true even if they seem to be at variance from commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts.

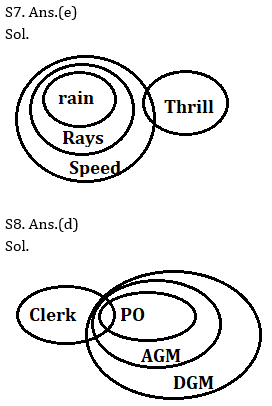
Q6. Statements:
Some studio are hall
All hall are room
Only room is bag
Conclusion:
I. Some bag are hall
II. Some studio are room
III. All Studio can be hall
(a) Only I is true
(b) Only II is true
(c) Both I and II is true
(d) Only III is true
(e) None of these

Q7. Statements:
All rain are rays
All rays are speed
Some speed are thrill
Conclusion:
I. Some rain are thrill
II. All speed are rays
III. No thrill is Rain
(a) Both I and III is true
(b) Both I and II is true
(c) Only I is true
(d) Only II is true
(e) None of these

Q8. Statements:
Some Clerk are PO
All PO are AGM
All AGM are DGM
Conclusion:
I. Some AGM are Clerk
II. All Clerk are DGM
III. All DGM can be Clerk
(a) Both II and III is true
(b) Only III is true
(c) Both I and II is true
(d) Both I and III is true
(e) None of these

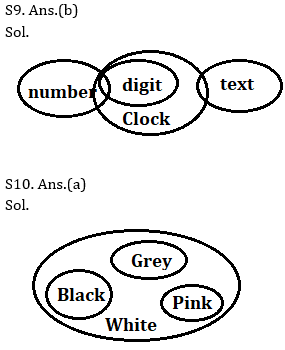
Q9. Statements:
Some number are digit
All digit are clock
Only a few clock are text
Conclusions:
I. All clock can be number
II. Some number are text
III. Some digit are text
(a) Only II follows
(b) Only I follows
(c) Only II and III follow
(d) Only III follows
(e) None follows

Q10. Statements:
All black are white
All grey are white
Only white is Pink
Conclusions:
I. Some Black can be grey
II. Some pink can be grey
III. All White can be Black
(a) Only I follows
(b) Only II and III follow
(c) Either I and III follow
(d) Only I and III follow
(e) None of these

Directions (11-15): In each of the questions below are given some statements followed by some Conclusions. You have to take the given statements to be true even, if they seem to be at variance from commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts.
(a) If only conclusion I follows.
(b) If only conclusion II follows.
(c) If either conclusion I or II follows.
(d) If neither conclusion I nor II follows.
(e) If both conclusions I and II follow.

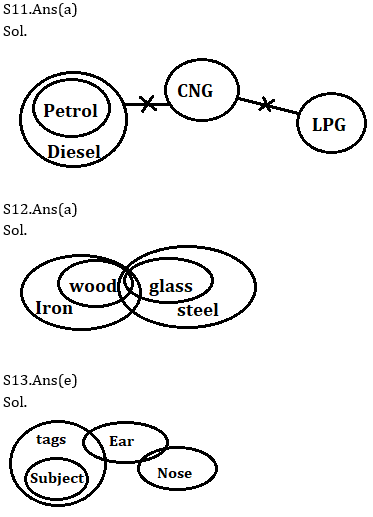
Q11. Statements:
All Petrol is Diesel
No Diesel is CNG
No CNG is LPG
Conclusion:
I: All LPG can be Petrol
II: Some Diesel are not LPG

Q12. Statements:
Only a few wood are glass
All wood are iron
All glass is steel
Conclusion:
I: All steel can be Iron
II: All iron can be glass

Q13. Statements:
Only tags are subject
Only a few tags are ear
Some ear are nose
Conclusions:
I. Some nose can be tags
II. All nose can be ear

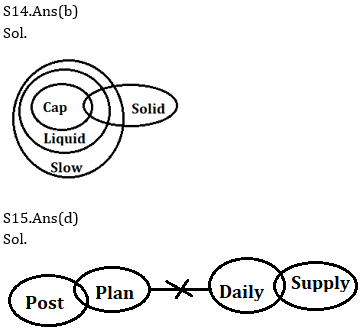
Q14. Statements:
All cap are liquid
All liquid are slow
Some cap are solid
Conclusions:
I. All slow are solid
II. Some liquid are solid

Q15. Statements:
Some post are plan
No plan is daily
Some daily are Supply
Conclusions:
I: Some post are daily
II: No supply is plan

Practice More Questions of Reasoning for Competitive Exams: