Quantitative Aptitude Quiz For ECGC PO 2021- 17th January

Table of Contents

Q1. Arun invested Rs. 10,000 for three years at CI at the rate of 20% per annum. If in 1st and 3rd year interest is calculated annually and in 2nd year it was calculated half-yearly, then find the total interest received by Arun in three years?
(a) Rs 7554
(b) Rs 7424
(c) Rs 7868
(d) Rs 7262
(e) Rs 7343

Q2. A certain money becomes 7/4th of itself in 6 years at a certain rate of simple interest. Find the rate of interest (in %).
(a) 25
(b) 30
(c) 12.5
(d) 6.25
(e)10

Q3. Difference between CI received in first 1.5 years (compounded annually) at 20% per annum and CI received in last 1.5 years when compounded half yearly at the same rate of interest on the same sum is Rs 715 then find the sum?
(a) Rs. 66,000
(b) Rs. 65,000
(c) Rs. 64,500
(d) Rs. 65,500
(e) Rs. 67,500

Q4. ‘A’ invested Rs. X on CI and ‘B’ invested Rs. Y on SI at the rate of 10% and 20% respectively. A invested for two years and B invested for three years and ratio of interest got by ‘A’ for second year and total interest got by B is 1 : 3. Veer invested Rs. (X + Y) on SI for two years on 12% p.a. and gets Rs. 372 as interest. Find (X – Y)?
(a) Rs. 350
(b) Rs. 450
(c) Rs. 400
(d) Rs. 750
(e) Rs. 800

Q5. Aman divided his total savings between his son and daughter in the ratio of 5 :3. His son invested his share on CI for two years at the rate of 10% and received the interest Rs. 480 less than his sister, who invested her share on SI for three years at the rate of 15% . Find Share of Aman’s son and daughter respectively?
(a) Rs. 10800, Rs. 2000
(b) Rs. 9600, Rs. 4200
(c) Rs. 8000, Rs. 4800
(d) Rs. 9800, Rs. 3000
(e) Rs. 7000, Rs. 5800

Q6. The C.I at a certain rate for Rs ‘X’ for 2 years is same as the S.I at the same rate for same Rs ’X’ for four years. Find the rate. (in % p.a)
(a)200
(b)300
(c)400
(d)500
(e)250

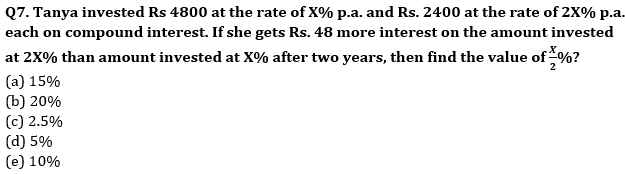
Q8. Veer invested an amount on simple interest, and it becomes two times of itself in 10 years. If Veer invested Rs. X at the same rate of interest on CI and he gets Rs. 5324 as amount after three years, then find amount invested by Veer (in Rs.)?
(a) 4400
(b) 3600
(c) 4800
(d) 4000
(e) 3000

Q9. Rahul invested a sum of Rs. 10000 in a scheme offering simple interest at 10% p.a. after 2 years, he again invested all the money he got from scheme in share market at Rs. 50 per share. After 1 month, he sold all his shares at Rs. 52 per share. Find his profit percent.
(a) 2 %
(b) 24 %
(c) 4 %
(d) 15 %
(e) 12 %

Q10. Sahil invested a sum of Rs. 4000 at 10% compound interest compounding annually while Sanjay invested 50% more than Sahil at 20% simple interest. Find the ratio of interest received by Sahil & Sanjay in second year.
(a) 11 : 60
(b) 7 : 20
(c) 7 : 10
(d) 11 : 20
(e) 11 : 30

Q11. A, B & C invested their respective savings in a scheme, which offered CI at 20% p.a. for two years and received total interest of Rs. 1694. If A & C invested double of their respective saving in another scheme, which offered SI at 10% p.a. for two years and received total interest of Rs. 1100, then find difference between saving of A & C together & saving of B?
(a) 1250 Rs.
(b) 1650 Rs.
(c) 1150 Rs.
(d) 1050 Rs.
(e) 750 Rs.

Q12 Interest earned on a certain sum in 2 years at 20% pa at CI is twice the interest earned on Rs. 1100 for 2 yrs at 10% SI. Find sum.
(a) Rs. 1000
(b) Rs. 500
(c) Rs. 750
(d) Rs. 1250
(e) Rs. 1500

Q13. If the compound interest on a certain sum for second year and compound interest for third year is in ratio of 5:6. What would be the total amount after 2 years at the same rate on Rs. 10000? (in Rs.)
(a) 14400
(b) 11000
(c) 11236
(d) None of these
(e)Cannot be determined

Q14. A sum of Rs. 1000 is lent partly at 10% and 15% at simple interest per annum. If total interest received after 3 years is Rs. 390. Find the amount lent at 10% rate.
(a) 100
(b) 900
(c) 600
(d) 400
(e)500

Q15. An amount is lent out at y% p.a at S.I for 2 years. If it had been lent at 2y% p.a at S.I for ‘a’ more years, then the interest would have been five times of the earlier interest. Find the value of ‘a’.(in years)
(a) 5
(b) 4
(c) 3
(d)2
(e) none of these

Practice More Questions of Quantitative Aptitude for Competitive Exams: