Pythagoras Theorem – Definition, Formula and Examples

A very common and important topic in Mathematics, Pythagoras Theorem, or the Pythagorean Theorem. It explains the relation between the different sides of a right-angled triangle. The theorem states that “In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides of the triangle.” 

Practice With,

• Bank Maha Pack Subscription (12 Months)
• Click Here to Visit Adda247.com for Study Material 

The other two sides here are the Perpendicular and the Base of the triangle. Therefore, in a right-angled triangle, the Hypotenuse becomes its longest side, since it is opposite to the 90° angle.  

FORMULA OF PYTHAGOREAN THEOREM

In a right-angled triangle, 

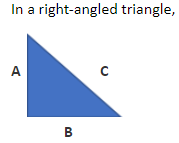
A is the Perpendicular

B is the Base

C is the Hypotenuse

Therefore, according to the definition of the Pythagorean Theorem, the formula would be:

Hypotenuse²= Perpendicular² + Base²

In other words, it would be:

C²= A²+ B²

Click Here to Register for Bank Exams 2020 Preparation Material

Also Read,

PROOF OF PYTHAGORAS THEOREM:

In a right-angled triangle, the base and the perpendicular together make up an angle of 90 degrees with each other. therefore, according to the Pythagorean Theorem, “the square of the hypotenuse is equal to the sum of a base square and perpendicular square.” 

In order to prove this theorem, 

Let us suppose a triangle ABC, which is right-angled at B. 

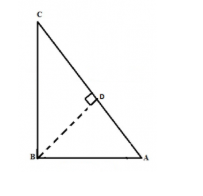
We have to prove that: AC²= AB² + BC²

To explain: We draw a perpendicular line BD which meets AC at D. 

Proof:

We know by the theorem that if a perpendicular is drawn from the vertex of the right angle to the hypotenuse of a right-angled triangle, then the two triangles on both the sides of the perpendicular are similar to each other as well as to the whole triangle. 

Therefore,

△ADB ~ △ABC

Hence,

AD/AB = AB/AC (Condition for similarity)

Or, AB² = AD × AC (1)

Also, △BDC ~△ABC (By applying the same theorem) 

Therefore,

CD/BC = BC/AC (Condition for similarity)

Or,

BC²= CD × AC (2)

Now, 

By adding the equations (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.

APPLICATIONS OF PYTHAGOREAN THEOREM

Some applications of the Pythagoras Theorem are:

1. To know whether the triangle is a right-angled triangle or not
2. To find the diagonal of a square
3. In a right-angled triangle, we can calculate the length of any side if we know the length of the other two sides

Frequently Asked Questions- Pythagoras Theorem

Q. How do you find the Pythagorean Theorem?

In a right-angled triangle, Hypotenuse²= Perpendicular² + Base²

Q. What is Pythagoras Theorem?

It is a fundamental theorem of Mathematics that defines the relationship between three sides of a right-angled triangle.

Q. What is the Pythagorean theorem in simple terms?

Simple definition of Pythagorean theorem is that the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides.

Q. How is the Pythagorean Theorem useful in real life?

This theorem is useful in architecture, construction projects, woodworking and other such projects, where you need to calculate the length of the diagonal connecting given two straight line.